■「ゼロから学ぶ物理の1、2、3」補足
以下は、
『朝日カルチャーセンターの講義でやったけれど、本には入っていない部分や質問の答えなど』
です。図は入っておりません。(手書きの下手な図なので見せたくない。あしからず。朝カルでは配ったけれど)
§的を射た質問
「線電荷が動くと電流になるという。線電荷だけだと電場だけ。それが動いて電流になると磁場ができるという。たしかにアンペールの法則から磁場は計算できる。だが、電荷が動くだけだと、電場も残るような気がするが?」
ええと、つまり、通常は、
・電荷→電場
・電流→磁場
ということですっきり理解していたのが、
・電荷が動くと電流
と考えてローレンツ変換を適用してみると、電線の場合に(アンペールの法則による)磁場だけでなく、余分な電場が出てきてしまうという問題。果たして電線のまわりには、磁場しかないのか? それとも電場もあるのか?
で、答えであるが、電線の場合、マイナス荷電の電子が動いているだけでなく、プラス荷電のイオンが止まっているのだ。そのため、電子だけを考慮すると、たしかに磁場だけでなく電場も存在するのだが、その電場は、イオンがつくる電場によって相殺されてしまう。
・電子が動く→磁場と電場
・イオンが止まっている→電場
・上の二つを足す→磁場だけが残る
これは、ちゃんと計算することができます。
(ただし、イオンの電荷密度をσとすると、動いている電子の電荷密度は(-σ)でなくてはいけない。実際の電線では、完全には相殺されないと思う。)
§電場と磁場の一覧表
さて、時間的に変動する電磁場の話は、もう少し先延ばしにして、まずは、電場のガウスの法則とアンペールの法則をつかって、教科書に出てくる代表的な電場と磁場の計算をやってみましょう。
なにしろ、抽象的な方程式を書いただけでは、応用が利かないからな。といっても、復習する場合、法則の適用法を思い出せばいいわけであって、すべての問題の演習をやる必要などない。だから、本当に代表的な例題を二つ三つやってみて、あとは、微分積分のところと同じように一覧表にしてしまおう。
まず、ガウスの法則をつかって電場を求めてみる。
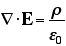
というのは、電荷ρによって電場Eの「発散」が生じる、という意味だった。一番カンタンなのは、ふつうの点電荷Qの周囲の電場だ。(図)物理学では問題を解くときに「対称性」を利用することが多い。点電荷が周囲につくる電場の場合、それが放射状になっていて、電荷の位置(原点)からの距離rだけの関数であることは明らかだ。なぜなら、原点に電荷をおいて、周囲を球面で囲ってみたとき、その球面上のどの点にもちがいはないから。それで、ガウスの法則の適用のしかただが、次のようにやる。
1 電荷の周囲を想像上の「袋」で包み込む
2 「袋」を垂直に貫く電場の成分をすべて足すと、それは、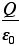 に等しい(Qは袋の内部の総電荷) に等しい(Qは袋の内部の総電荷)
これは、実は、これまでやってきたガウスの法則を「積分」することにあたる。「足す」というのは、ぶっちゃけた話、「積分する」という意味だからだ。つまり、これまで出てきた電荷のρは、本当は、「電荷密度」のことだったわけ。(コラム参照)
まあ、意味からいえば、発散した電場をすべて「袋」で捕まえて足してやると、その源の総量Q(をε0で割ったもの)になる、ということなので、ナットクしていただけることと思う。いかがでしょう?
この図の場合、袋の形状を完全な球面にするのが得策だ。なぜなら、そうすれば、すべての電場が袋と垂直に交わるから、余計な手間が省ける。いちいち、垂直な成分を計算するのは面倒だ。(垂直な成分をとりだすというのは、数学的には、内積をとる、ということです。コラム参照)
球面の半径をrとすると、電場は、
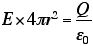
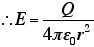
と、求まる。
ありゃま。これって、どこかで見たような・・・。そうです。クーロンの法則ではありませんか。点電荷から距離rの地点における電場の式だから、一致するのはあたりまえ。ようするに、クーロンの法則というのは、ガウスの法則の特別な場合なのだな。フムフム。
次にいこう。
無限に大きいシートに面密度σの電荷が分布している場合。ようするに1m2あたりσクーロンという意味だ。今度も対称性から、電場は、シートに垂直な方向にしか存在しないことがわかる。なぜなら、図のように、斜めの成分は、必ず相殺されるからだ。物理学の計算においては、とにかく、対称性を見破ることによって、計算をカンタンにするのがコツなのだ。最終的にゼロになるのが明らかな部分を延々と計算していては時間の無駄。
で、今度は、電場を包み込む「袋」は、シートに平行な面と垂直な面をもったものなら何でもよい。(図)
シートに平行な面の面積をSとすると、袋の中の電荷の総量はσSなので、電場は、
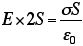
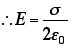
と、求まる。電場は上下に出ているので、「袋」を貫く面積は、Sではなく、2Sになることに注意。この問題を応用すると、二枚のシートの間の電場も求めることができる。ただし、シートの電荷は符合が逆だとする。つまり、コンデンサーのような場合である。単純に重ね合わせればいいので、コンデンサーの外側では、電場が相殺してゼロになる。コンデンサーの間では、電場が2倍になって、
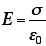
という次第。
なお、これと紛らわしいが、導体の表面の電場は、図のような「袋」を考えることによって、
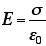
であることがわかる。なぜなら、導体の場合、電場は外に向けて出ているが、内部には存在しないからである。
まあ、こんなふうに工夫しながら計算してゆく。復習本という性格上、あらゆる計算を詳しくご紹介できないので残念だが、代表的な電場を一覧表にしておきます。
(一覧表)
磁場の場合は、ガウスの法則ではなく、アンペールの法則、
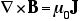
をつかって計算することになる。今度は「発散」ではなく「回転」なので、「袋」の代わりに「輪」を考える。想像上の円に乗っている磁場を足しあげるのである。
といっても抽象的で意味不明なので、具体例をやってみましょう。一番カンタンなのは、無限に長い直線電流だ。電線から距離r離れた場所の磁場は、
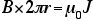
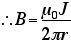
と、計算できる。ね、カンタンでしょ?
次は、図のようなシートを面密度σvの電流が流れている場合。ネタバレ的に電流の表面密度をσvと書いた。その理由は、すぐに判明します。とにかく、計算してみよう。対称性から、磁場は、シートに水平な成分しかないことがわかる。ええと、わかりにくい人は、前の問題の電線をたくさん並べたのだと考えてください。環状の磁場を電線の幅だけずらしながら並べてゆくと・・・たしかに、余計な成分は相殺されて、シートに平行な磁場しか残らないようだ。
で、平行な部分の長さをlとして、四角い経路を考える。すると、シートの長さlに間には、(σv×l)だけの電流が含まれるから、
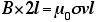
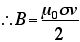
という具合に磁場が計算できる。
さて、「回転」なのに「円」ではなく「長方形」の経路に沿って磁場を足しあげたのだが、これは、数学的には「線積分」というものなので、これでかまわない。電場のガウスの法則のときに、どんな「袋」で電荷を包んでもよかったのと同じで、磁場のアンペールの法則の場合、どんな「輪」で一周してもかまわないわけ。ただし、線の接戦方向の成分を足しあげるのである。
こういうのは、万事、対称性に注目して、いちばん計算がカンタンになるような「袋」や「輪」の形状を選ぶべきなのだ。それよりも、注目すべきは、シートの電場と磁場の式の類似性である。もう一度、書いておくと、シートの電場は、
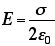
だった。この式は、磁場の式と、
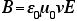
という関係で結ばれている。ちょっとみにくいので、
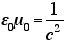
をつかうと、これは、
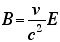
と、書くことができる。つまり、
「磁場は電場に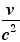 をかけたもの」 をかけたもの」
になっている。これは、なにか、意味があるのだろうか? そこで、代表的な磁場の一覧表をご覧ください。
(磁場の一覧表)
もう、答えを書いてしまったわけだが、なんと、ある形状の物体の電場を求めたら、それに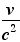 をかけると、同じ形状の物体を電流が流れているときの磁場になるのだ。 をかけると、同じ形状の物体を電流が流れているときの磁場になるのだ。
ただし、表の最後をご覧になるとおわかりのように、大きさだけを問題にしているのなら、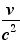 をかけるだけでいいが、方向も考慮すると、どうやら、ベクトルの外積になるらしい。つまり、 をかけるだけでいいが、方向も考慮すると、どうやら、ベクトルの外積になるらしい。つまり、
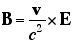
になっているらしい。
ポイント 磁場は、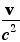 と電場の外積になる と電場の外積になる
ある意味、これが電場と磁場をまとめて「電磁場」と呼ぶことの真の理由なのだ。電荷がσだとすると、それに電荷の速度vをかけたものは、電流である。電荷があると電場が生まれる。電流があると磁場が生まれる。電荷を動かせば電流になるのであれば、ようするに、電場と磁場のちがいは、止まっているか動いているかの差にすぎない。だから、電場と磁場の間に緊密な関係があっても不思議ではない。
ええと、このお話は、一時、中断して、次の節では、マックスウェルという人のどこがエラかったのかを理解するために、「変位電流」の意味を考えてみよう。それがおわったら、空飛ぶ電磁場の概略をお話しして、いよいよ、電磁場の復習のクライマックスへと突入いたします。
<コラム>微分法則と積分法則
なんだか変だ。マックスウェルの方程式に出てくる「電場のガウスの法則」をつかって電場の計算をやったわけだが、もともとの法則は微分の恰好をしているのに、どうして、広い範囲の電場を求めることができたのだろう。
微分=局所的
積分=大局的
というイメージがあるが、大きな「袋」で電荷を包むのなんて、どう考えても大局的なお話のように思われる。
ストーリーのどこかにギャップがあるはしないか?
バレたか。
慧眼な読者にはかなわないので、手短に解説いたしましょう。実は、ここの計算でつかったのは、ご指摘のとおり、電場のガウスの法則の積分形なのである。それは、こんな恰好をしている。
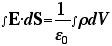
まったくもって意味不明かつ抽象的な積分にみえるが、右辺のほうは、単に体積V(Volume)にわたって電荷密度ρを積分した(=足しあげた)だけ。
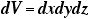
なので、実際は、三重積分ということになるが、その体積の表面(=「袋」)より内側に存在する総電荷をQとかけば、右辺は、
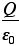
ということだ。ようするに、Qは、「袋の中の全電荷」ということである。
さて、やっかいなのは左辺のほうだ。これは、dSのSが「surface(表面)」の頭文字であることから推測できるように、二重積分である。ただし、「袋」の全表面について足しあげないといけない。すでに法則を適用しているのだから、その恰好が立方体とか球でかまわないことは、ご理解いただけるだろう。ここでは、図のような立方体を考える。(図)
「袋」というより「箱」だな、これは。それで、この箱に電場が入って、出ていく状態を思い浮かべる。(図)
まず、上下方向に注目すると、箱の上の面から外に出る電場の「束」は、
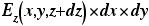
だと考えられる。電場は位置の関数であり、これは、
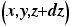
という点における電場のz成分の値に、箱の上面の面積、
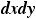
をかけたものである。箱の下面では、同じように、
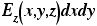
になるが、マイナスがつく。なぜなら、微小面積dxdyには「向き」があるからである。箱の表面から外向きに「面積ベクトル」が突き出ているのである。面積ベクトルというのは、その面積の大きさ(=矢の長さ)をもったベクトルのことである。
箱の上面と下面とでは、当然のことながら、方向が逆だから、マイナスがつくことになる。(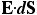 というのは、内積なのである。) というのは、内積なのである。)
正味、z方向では、
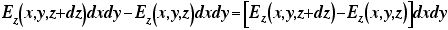
という電場の流入と流出があることになる。ところが、
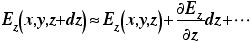
と、テイラー展開できるので、結局、
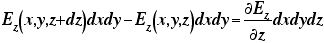
が、上下面の電場の出入りの収支ということになる。これは、横のx方向やy方向でも同様なので、箱全体の収支は、
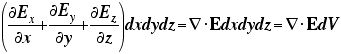
になる。ここで、このコラムの冒頭の、
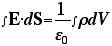
という式に戻る。ようするに、左辺は、
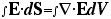
なのであり、これを右辺と比べてみると、すぐに、
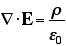
であることがわかる。あまり厳密にやっていないので、大変、恐縮だが、こういうことである。
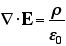 を積分すると を積分すると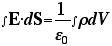 になる になる
つまり、ガウスの法則の微分形と積分形は、物理学的に同等ということである。ちなみに、
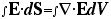
という公式は、電場でなくても成立する。これは、ようするに、面積分を体積積分(あるいは、その逆)に変換する公式であり、「ガウスの定理」と呼ばれている。数学的な同値関係である。この数学の定理に「電荷が発散の源になる」という物理を加味すると、ガウスの法則になるのである。定理は数学で、法則は物理ということです。
ガウスの定理は、覚えにくいかもしれないので、物理学流に次元を勘定して、覚えやすくしてみよう。
左辺の積分は、dSの部分がdxdyなどという微小面をあらわすので、長さの2乗の次元をもっている。右辺のdVは、dxdydzという微小体積をあらわすので、長さの3乗の次元をもっている。このままだと、左右の次元の勘定が合わない。
そこで、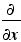 という、分母に長さの次元をもつ∇が必要になる。また、電場Eはベクトルなので、他のベクトルとの内積をとる必要がある。dSは方向が定義できるからベクトルだが、dVはベクトルではない。 という、分母に長さの次元をもつ∇が必要になる。また、電場Eはベクトルなので、他のベクトルとの内積をとる必要がある。dSは方向が定義できるからベクトルだが、dVはベクトルではない。
こんなふうに分析してみると、ガウスの定理の恰好は、おのずから決まってくる。試験のときに忘れたら、こうやって、次元を分析してみれば正しい形が推測できるのだ。
さて、あまりコラムが長くなると嫌なので、駆け足で結果だけ紹介しておくが、アンペールの法則のほうは、数学のストークスの定理をつかって、微分形と積分形の変換ができる。ストークスの定理は、
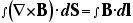
という具合に面積分と線積分を変換する。

|
|