・円周率
「円周率」という何気ない言葉ですが、みなさん、その意味をご存じでしょうか? 円周の率・・・いったい何の率なのでしょう?
これは、もちろん、円周と直径の比率のことです。直径は半径rの2倍ですから、円周率をπと書くと、
π=円周÷(2r)
になります。いいかえると、
円周=2πr
ということです。
円周率を求めるために、円を多角形で近似してみましょう。たとえば、(かなり乱暴ですが)円を正方形で近似してみます。
円の外側と内側に正方形を描けばいいのです。
すると、円周は正方形の外周で置き換えられます。正方形での近似には二種類あります。円に内接する正方形と円に外接する正方形です。内接する正方形の外周は、一辺が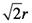 なので、それを4倍して、 なので、それを4倍して、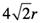 になります。ですから、 になります。ですから、
π=外周÷(2r)=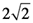 =約2.828 =約2.828
と計算できます。一方、外接する正方形で計算すると、同様にして、
π=4
と計算できます。帯に短し、襷に長し。実際のπの値は、もちろん、この二つの値の中間にあります。
そこで、この正方形の角の数を増やして、どんどん円に近い多角形にして、近似の度合いを高めるのです。そして・・・正13万1072角形で近似したときに、初めて、関孝和が求めた円周率の近似値が求められるのです! かなり凄いことではありませんか?
・量子テレポーテーション
量子の世界には「からみあい」という奇妙な現象があります。
ある量子と別の量子がからみあっている場合、その二つをどれだけ引き離しても、からみあいは解けません。ふつうの粒子であれば、くっついているときには互いに影響しあえますが、何万キロメートルも引き離したら、もはや関係がなくなってしまいます。ですが、量子の場合は、いくら離れても「つながっている」のです。
この現象は実証されています。ということは、もしかしたら「離れている」いうわれわれの「空間」の概念のほうが一種の幻なのかもしれません。
閑話休題(それはさておき)。
テレポーテーションは「遠隔移動」という意味で、通常の粒子ではSFの世界のお話にすぎませんが、量子の場合は、科学的にテレポーテーションが実証されています。
量子テレポーテーションを理解するには、ご家庭のファックスと比べてみるのが一番です。
ファックスの場合、電話回線を通して、オリジナルの原稿を遠隔地に送ります。しかし、原稿そのものが送られるわけではありません。オリジナルの原稿は送り手のところに残ります。原稿の「情報」が電気信号に変換されて、それが相手のファックスに入っている白紙に印刷されるだけなのです。その際、オリジナルがもっていた情報は、少し劣化します。(劣化というのは、ようするにファックスがオリジナルよりも見にくくなる、という意味です。)
量子テレポーテーションの場合、オリジナルの量子は、「からみあい」という回線を通して、遠隔地に送られます。相手のところには、オリジナルの量子と寸分たがわないものが出現します。情報は全く劣化しません。そして、送り手の元にあったオリジナルは破壊されてしまいます。
量子テレポーテーションでは、実際に量子が途中経路を移動しているわけではありませんが、「からみあい」という回路を通じて、オリジナルがもっていた全情報が相手のところに移動するのです。
量子とは、かくて、実体のある「モノ」というよりは、むしろ形のない「情報」のような存在だといえるでしょう。
・ミニブラックホール
もともと宇宙論学者のスティーブン・ホーキングが提唱した概念です。
ブラックホールにもいろいろな大きさのものがあります。
われわれの銀河の真ん中には、太陽の重さの百万倍とか十億倍といった超巨大なブラックホールがあることがわかっています。他の銀河の真ん中にも巨大ブラックホールがあります。
また、太陽よりも数倍から十五倍くらい大きな恒星は、寿命が尽きるとブラックホールになることがわかっています。これは普通サイズのブラックホールです。
ミニブラックホールは、そういった銀河や星のレベルよりもずっと小さなブラックホールで、これまでに誰も発見していませんが、理論的に存在が予言されているものです。
本文中で健史がミニブラックホールに言及しているのは、「ブラックホールの中に入ると、宇宙のまったく別の場所につながっている可能性がある」ということを暗にほのめかしているのです。通常、宇宙のある場所と別の場所をつなぐ「時空のトンネル」のことは「ワームホール」(=虫喰い穴)と呼びますから、健史の発言は、「あの猫は、ワームホールでも作るんですかね」でもいいかもしれません。
・行列式
行列式は、おそらく理系の大学に進むと数学の「線形代数」という授業で教わる概念であり、日常生活とはほとんど無縁の存在でしょう。
以下、数字や計算の細かい点は気にせず、行列式の役割だけ理解していただければと思います。(この本は数学の教科書ではありませんので!)
次のような連立方程式を考えてみましょう。
3x+y=7
x+2y=4
これを線形代数の授業では、
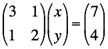
と、まとめて書いてしまいます。このカッコのことを「行列」と呼びます。そして、この式の両辺に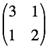 という行列の逆行列をかけて、連立方程式を一挙に解いてしまうのです。(逆行列は、ふつうの数の場合の逆数を一般化した考え方です。3に逆数の1/3をかけると1になりますよね? それを4つの数に対していっぺんにやってしまうのです。) という行列の逆行列をかけて、連立方程式を一挙に解いてしまうのです。(逆行列は、ふつうの数の場合の逆数を一般化した考え方です。3に逆数の1/3をかけると1になりますよね? それを4つの数に対していっぺんにやってしまうのです。)
その逆行列をもとめる際に「行列式」が登場します。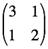 の行列式は、 の行列式は、
3×2−1×1=6−1=5
です。そして、逆行列は、
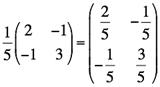
になります。この逆行列を
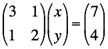
の両辺にかけると、行列のかけ算の約束により、
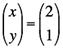
となって、一気に答えが出るのです。
この方法は、一見、二つの方程式をバラバラにして解く、ふつうのやり方よりも面倒くさいようですが、馴れてしまえば、ずっと早く計算ができるようになります。また、パソコンで解くときにも威力を発揮します。
この行列式には、しかし、もっと別の直観的な意味もあります。それは、「面積」や「体積」という意味です。(川辺さま、以下、別紙へと続きます)
・関孝和(せき たかかず)寛永十七年(一六四二年)〜宝永五年(一七〇八年)
関孝和は、今の群馬県、上野の国の藤岡で生まれました。幕臣の家でしたので、彼は武士の家系ということになります。幼少の頃から、当時のベストセラー数学書「塵刧記」を独学で学んだというのですから、数学に関して突出した才能を持ち合わせていたのでしょう。
当時、日本での数学はそろばんや算木(ギリシャ数字のような表記で数を表し、算盤と呼ばれる表と共に用いて、代数の方程式の解などを求めるのに使われたもの)を使うのが一般的でしたが、関孝和は筆算によって代数の計算を行う方法を発明し、和算を高等数学へと発展させる基礎を作った人物です。
ただ、和算の手法は主に各々の流派の中で、師弟関係を通じて継承されたので、一般に広く伝わるものではありませんでした。それでも、微分積分などの分野は西洋と同時期に発展し、分野によっては、西洋に先んじていたものもあるのです。
ベルヌーイ数は現代数学の難問と深くかかわっています。その計算は比較的簡単ですが、その「意味」を説明するのはきわめて難しく、それこそ本が一冊書けてしまいます。ここでも解説はしませんが、「リーマン予想」という数学の未解決の難問とも関係している、とだけ述べておきましょう。
ところで、関孝和以前の日本に数学がなかったわけではありません。七世紀頃には遣隋使、遣唐使が中国から文化を持ち帰り、八世紀には「算博士」という官職がありました。また、万葉集にも九九についての歌が収められており、政治や貴族階級の間では、算数や数学が用いられていたことが知られています。ただし、それが庶民の間にまで広まるには、江戸時代を待たなくてはなりませんでした。
ちなみに本文中で出てくる「算額」は、江戸時代の中期頃からその風習が始まりました。絵馬をもっと大きくしたようなもので、神仏に数学の問題が解けたことを感謝し、さらなる勉学の向上を祈願して奉納されたものと考えられています。また、神社仏閣は人の集まるところですので、そこに自分が編み出した問題を、解答をつけずに奉納し、それを見た誰かがそれを解き、解答を算額にして奉納する、などということもありました。この「算額」は日本独自の文化で、他の国に同じような例は見られません。
ただ、香鈴という名前が江戸時代にあったか、そして、関孝和が算額を奉納しようと用意していたかどうかについては、作者の与り知らぬところでございます。
寛永一七年(一六四二年) 上野国 藤岡に幕臣の子として生まれる。後に六代将軍綱豊の直参として江戸詰めとなる。
延宝二年(一六七四年) 「発微算法」発刊 点竄術(てんさんじゅつ)(代数の筆算による計算法)を発明
天保三年(一六八三年) ライプニッツに先駆けて、独自に行列式の概念を研究。また、ベルヌーイよりも先にベルヌーイ数を発見した。
宝永五年(一七〇八年)十月二十四日(旧暦) 病没
|
|
|
|